Semana 1: 30 - 09- 2014
Instrucciones de la Materia de Matemática Avanzada
Indicaciones para la creación del Blog.
Plan Microcurricular de la asignatura.
Plan Microcurricular de la asignatura.
SEGUNDA SEMANA 07-10-2014
Los Número Complejos
Un número complejo es un número de la forma a + bi, donde a y b son números reales, llamados parte real y parte imaginaria respectivamente, e i es la unidad imaginaria que se define como

Ejemplo:

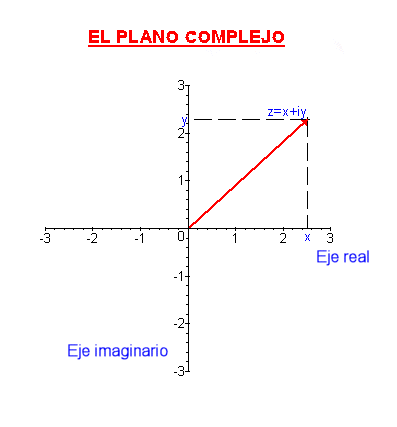

Módulo de un complejo ( r )

---------------------------------------------------------------------------------------


 .
.

z1=|z1|⋅[cos(α)+i⋅sin(α)]
z2=|z2|⋅[cos(β)+i⋅sin(β)]
z1⋅z2==|z1|⋅[cos(α)+i⋅sin(α)]⋅|z2|⋅[cos(β)+i⋅sin(β)]|z1|⋅|z2|⋅[cos(α)⋅cos(β)−sin(α)⋅sin(β)+ i⋅(cos(α)⋅sin(β)−sin(α)⋅cos(β))]
z1⋅z2=|z1|⋅|z2|⋅[cos(α+β)+i⋅sin(α+β)]
(|z|⋅[cos(α)+i⋅sin(α)])n=
=(|z|⋅[cos(α)+i⋅sin(α)])⋯(n)(|z|⋅[cos(α)+i⋅sin(α)])=
=|z|n⋅[cos(nα)+i⋅sin(nα)]
R y ϕ respectivamente, siempre tiene raíces enésimas, y precisamente el número de éste es n .
(|z|⋅[cos(α)+i⋅sin(α)])n=R⋅[cos(ϕ)+i⋅sin(ϕ)]
|z|n=R y nα=ϕ+k⋅360∘
|z|=R−−√n
Se tiene pues que |z| es la raíz enésima aritmética de R .
α=ϕn+k⋅360∘n
ϕn, ϕ+360∘n, ϕ+2⋅360∘n, ϕ+3⋅360∘n, … , ϕ+(n−1)⋅360∘n

Propiedades de la derivación de números complejos


Ejemplo:
x2 + 9 = 0

La representación de un número complejo en el plano sería: la parte imaginaria en el eje Y y la parte real en el eje X.

Observaciones:Sea z=a+bi
- Si Re(z)=a=0, entonces z es un imaginario puro
- Si Im(z)=b=0, entonces z es un número real
Igualdad de Complejos:
Dos números complejos son iguales si lo son las partes reales e imaginarias respectivamente:
a + b i = a ' + b ' i ⇔ a = a ' y b = b '
Operaciones:
Suma y diferencia de números complejos
(a + bi) + (c + di) = (a + c) + (b + d)i
(a + bi) − (c + di) = (a − c) + (b − d)i
Propiedades
- Clausurativa
- Conmutativa
- Asociativa
- Distributiva
- Existencia del neutro multiplicativo
- Existencia del inverso multiplicativo
Producto de números complejos
(a + bi) · (c + di) = (ac− bd) + (ad + bc)i
Sea :
i0 = 1
i1 = i
i2 = −1
i3 = −i
i4 = 1
. .
. .
Cociente de números complejos Inverso de Complejos
Inverso de Complejos
Dado Z=x+iy, entonces el opuesto aditivo de Z es:
-x-iy
-x-iy
Conjugada de un complejo
Sea z= a + bi, entonces el conjugado de Z es a-bi
El ángulo se llama "Argumento de Z" y es igual al arc tan ( b / a )
Forma Polar de un número complejo
Sea:
El Argumento de un complejo es el ángulo que forma el vector con el eje real. Se designa por arg(z).
|
 .
.
La forma polar sería: z = rα
Inverso multiplicativo de Z

Propiedades
- | Z . W | = | Zl . lW|
- |Z/W|=|Z|/|W|
- | Z + W | <= | Zl + lWl
Forma trigonométrica de un número complejo
| trigonométrica | z = r (cos α + i sen α) z = r cis α |
|---|
Sea cis α = cos α + sen α i
Producto:
Si escribimos dos números complejos:
Cuando se haga el producto, quedará:
Sabiendo la fórmula del coseno de la suma y la del seno de la suma se obtiene:
División:
z1z2=|z1|⋅[cos(α)+i⋅sin(α)]|z2|⋅[cos(β)+i⋅sin(β)]=|z1||z2|⋅[cos(α−β)+i⋅sin(α−β)]
Potenciación:
Consideramos el producto de n números complejos en forma trigonométrica:
Esta fórmula es la que nos da la potencia enésima de un complejo en forma trigonométrica y se debe a Moivre.
Radicación:
Dado un número complejo cualquiera cuyo módulo y argumento representaremos por
En virtud de la definición, la condición para que |z|⋅[cos(α)+i⋅sin(α)] sea una raíz enésima es:
Entonces, los dos números representados por el primer y segundo miembro de ésta igualdad han de ser iguales, por lo tanto, deberán tener el mismo módulo y sus argumentos deberán diferir en un número exacto de circunferencias, es decir:
El módulo |z| de la raíz buscada, queda perfectamente determinado por la primera de éstas ecuaciones, ya que ha de ser un número positivo cuya potencia enésima iguale a R , así:
En cuanto al argumento α , la segunda ecuación nos da que:
A primera vista podría parecer que α tiene infinitos valores, pero en realidad, para k=0 hasta k=n−1 se obtendrak se obtiene los mismos números complejos que ya se encontro, dado que serán los mismos pero con algunas vueltas enteras más.
En resumen, todo número complejo no nulo R⋅[cos(ϕ)+i⋅sin(ϕ)] tiene n raíces enésimas distintas, cuyo módulo que es el mismo para todas (es igual a la raíz enésima aritmética del módulo R ) y cuyos argumentos (salvo múltiplos de 360∘ ) son:
-------------------------------------------------------------------------------------------------------
TERCERA SEMANA 14-10-2014
Función de Variable Compleja
El conjunto de salida y de llegada son los complejos.
Para encontrar la imagen de una función compleja , se lo realiza tal y como se lo realizaba en las funciones reales.
Límites
Sea f : C --> C
z --> f(z)
de dice que
para el caso de los complejos cambia el entorno, aquí el entorno es un disco... y su dominio de este disco.
-------------------------------------------------------------------------------------------------------------------------------------------------------
CUARTA
SEMANA 21-10-2014
Continuidad
Se observa que los números complejos se los podía representar de una nueva forma, la cual era a traves de la serie de Euler.
Esto se puede representar gráficamente de la siguiente forma:
Logaritmo Complejo
Sea z=reiӨ
ln z =ln (reiӨ)
w = ln z = ln r +iӨ ------> Valor principal (cuando k=0)
ln z =ln r +i(Ө+2πk)------> Valor General
Propiedades
ln z =ln (reiӨ)
w = ln z = ln r +iӨ ------> Valor principal (cuando k=0)
ln z =ln r +i(Ө+2πk)------> Valor General
Propiedades
DERIVACIÓN DE FUNCIONES DE VARIABLE COMPLEJA
La derivada de una función de variable compleja está definida y cumple las mismas propiedades que la derivada de una función real y se define de la siguiente manera:

Propiedades de la derivación de números complejos
FUNCIÓN ANALÍTICA U HOLOMORFA
- Una función f(z) es analítica (u holomorfa) en un abierto A si posee derivada en todo punto de A.
- Cuando se dice que una función f es analítica en un conjunto S que no es abierto, quedará sobrentendido que f es analítica en algún abierto que contiene a S.
- Cuando decimos que una función es analítica en un punto z0 , la derivada debe existir en todos los puntos de algún entorno de z0
- Si una función de la forma: f(z)= u(x,y) + i v(x.y), y si cumplen las ecuaciones de Cauchy- Riemann entonces la función es analítica y entera
Las ecuaciones de Cauchy-Riemann son dos ecuaciones diferenciales parciales que son básicas en el análisis de funciones complejas de variable compleja, debido a que su verificación constituye una condición necesaria para la derivabilidad de este tipo de funciones.
Sea la funcion: f (z) = u(x,y) + iv(x,y)
Si la función f(z) es derivable en un punto zo= xo + iyo entonces deben verificarse las condiciones de Cauchy-Riemann:





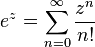





No hay comentarios:
Publicar un comentario